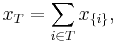Rado's theorem (Ramsey theory)

Rado's theorem is a theorem from the branch of mathematics known as Ramsey theory. It is named for the German mathematician Richard Rado. It was proved in his thesis, Studien zur Kombinatorik.

Let Ax = 0 be a system of linear equations, where A is a matrix with integer entries. This system is said to be r-regular if, for every r-coloring of the natural numbers 1, 2, 3, ..., the system has a monochromatic solution. A system is regular if it is r-regular for all r ≥ 1.

Rado's theorem states that a system Ax=0 is regular if and only if the matrix A satisfies the columns condition. Let c_i denote the i-th column of A. The matrix A satisfies the columns condition provided that there exists a partition of the column indices C₁, C₂, ..., C_n such if 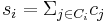$s_i = \Sigma_{j \in C_i}c_j$ , then

s₁ = 0
for all i ≥ 2, s_i can be written as a rational^[1] linear combination of the c_j's in the C_k with k < i.

Folkman's theorem, the statement that there exist arbitrarily large sets of integers all of whose nonempty sums are monochromatic, may be seen as a special case of Rado's theorem concerning the regularity of the system of equations

$x_T = \sum_{i\in T}x_{\{i\}},$

where T ranges over each nonempty subset of the set {1, 2, ..., x}.^[2]

References

^ Modern graph theory by Béla Bollobás. 1st ed. 1998. ISBN 978-0-387-98488-9. Page 204
^ Graham, Ronald L.; Rothschild, Bruce L.; Spencer, Joel H. (1980), "3.4 Finite Sums and Finite Unions (Folkman's Theorem)", Ramsey Theory, Wiley-Interscience, pp. 65–69 .